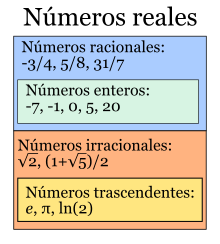
Número real
 .
.Números irracionales
Un número irracional es un número que no se puede escribir en fracción - el decimal sigue para siempre sin repetirse.
Ejemplo: Pi es un número irracional. El valor de Pi es
Números como 22/7 = 3.1428571428571... se acercan pero no son correctos.
3.1415926535897932384626433832795 (y más...)
Los decimales no siguen ningún patrón, y no se puede escribir ninguna fracción que tenga el valor Pi. Números como 22/7 = 3.1428571428571... se acercan pero no son correctos.
Números irracionales famosos
 | Pi es un número irracional famoso. Se han calculado más de un millón de cifras decimales y sigue sin repetirse. Los primeros son estos: 3.1415926535897932384626433832795 (y sigue...) | ||||
 | El número e (el número de Euler) es otro número irracional famoso. Se han calculado muchas cifras decimales de e sin encontrar ningún patrón. Los primeros decimales son: 2.7182818284590452353602874713527 (y sigue...) | ||||
 | La razón de oro es un número irracional. Sus primeros dígitos son: 1.61803398874989484820... (y más...) | ||||
 | Muchas raíces cuadradas, cúbicas, etc. también son irracionales. Ejemplos:
Pero √4 = 2, y √9 = 3, así que no todas las raíces son irracionales. |
Función inyectiva
En matemáticas, una función  es inyectiva si a cada valor del conjunto
es inyectiva si a cada valor del conjunto  (dominio) le corresponde un valor distinto en el conjunto
(dominio) le corresponde un valor distinto en el conjunto  (imagen) de
(imagen) de  . Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.
. Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.
Así, por ejemplo, la función de números reales , dada por
, dada por  no es inyectiva, puesto que el valor 4 puede obtenerse como
no es inyectiva, puesto que el valor 4 puede obtenerse como  y
y 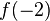 . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función
. Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  entonces sí se obtiene una función inyectiva.
entonces sí se obtiene una función inyectiva.
 es inyectiva si a cada valor del conjunto
es inyectiva si a cada valor del conjunto  (dominio) le corresponde un valor distinto en el conjunto
(dominio) le corresponde un valor distinto en el conjunto  (imagen) de
(imagen) de  . Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.
. Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.Así, por ejemplo, la función de números reales
 , dada por
, dada por  no es inyectiva, puesto que el valor 4 puede obtenerse como
no es inyectiva, puesto que el valor 4 puede obtenerse como  y
y 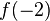 . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función
. Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  entonces sí se obtiene una función inyectiva.
entonces sí se obtiene una función inyectiva.Función biyectiva
En matemática, una función  es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
Formalmente,
 es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.Formalmente,




No hay comentarios:
Publicar un comentario