Funciones de variable real
Si la función 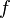 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función 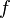 tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
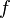 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función 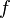 tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
|
Esto, escrito en notación formal:
Lo importante es comprender que el formalismo no lo hacen los símbolos matemáticos, sino, la precisión con la que queda definido el concepto de límite. Esta notación es tremendamente poderosa, pues, nos dice que si el límite existe, entonces se puede estar tan cerca de él como se desee. Si no se logra estar lo suficientemente cerca, entonces la elección del δ no era adecuada. La definición asegura que si el límite existe, entonces es posible encontrar tal δ.
No obstante, hay casos como por ejemplo la función de Dirichlet  definida como:
definida como:
 definida como:
definida como:
donde no existe un número c para el cual exista  . Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto números racionales como irracionales.
. Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto números racionales como irracionales.
 . Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto números racionales como irracionales.
. Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto números racionales como irracionales.
 existe un
existe un  tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.

No hay comentarios:
Publicar un comentario